Overcurrent grading is generally a "straight forward" consideration of the maximum fault current of a downstream relay should result in a slower operation for the upstream relay.

However Delta-star transformers have a particular special consideration.

Consider a 11/11 kV  Dyn transformer (1:1 transformer for direct comparison HV to LV)

Assume 500 turns secondary on the phase-to-neutral winding.

LV volts per turn = (11000/√3) / 500 = 12.7 V/turn

On the HV delta side, there must be the equivalent V/turn = 12.7 V/turn, but the winding is connected phase-to-phase. 
Hence for a 1:1 transformer to achieve 11 kV at 12.7 V/turn, there must be 866 turns on the HV windings.

T_HV  = (√3 / 2) x  T_LV = 0.866 T_LV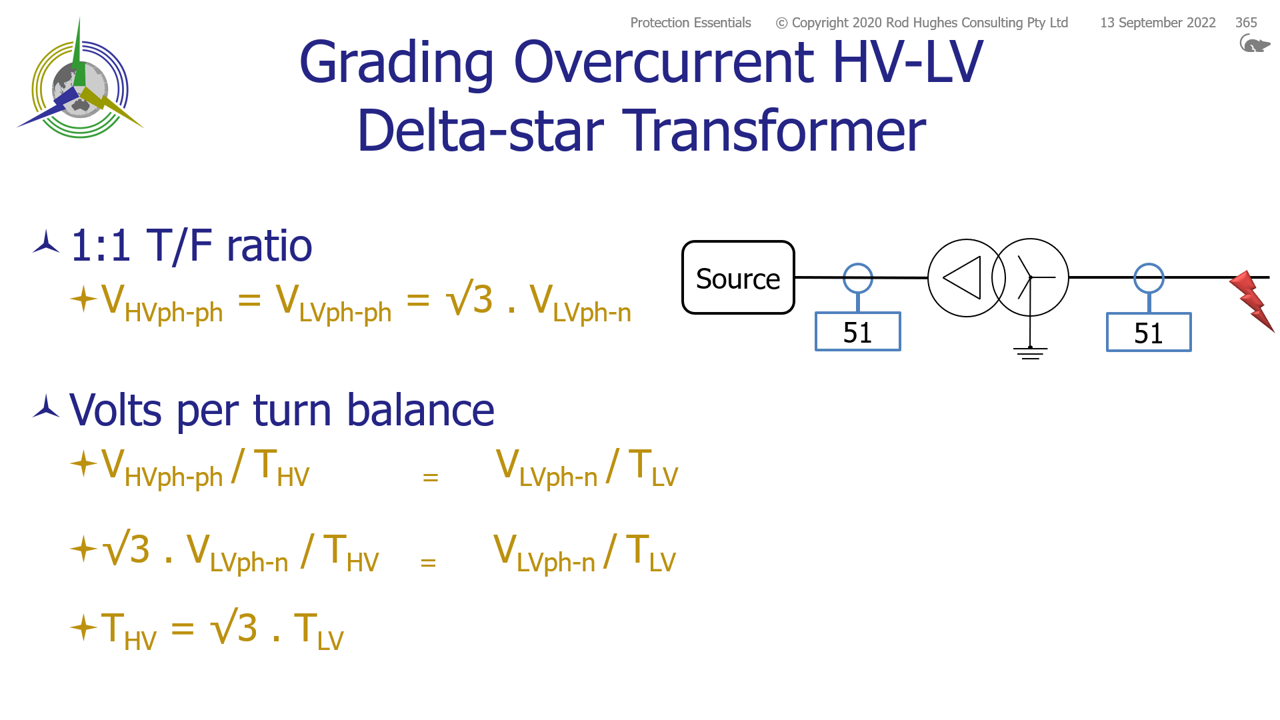

Lets assume the maximum LV phase-earth fault I_fmaxPh-N  = 1000 A.
In other words, that means the TF winding impedance is Xt = (11000/√3) / 1000 = 6.35 Ω

We can now consider the maximum fault current on the LV side for single phase to earth vs phase-to-phase faults.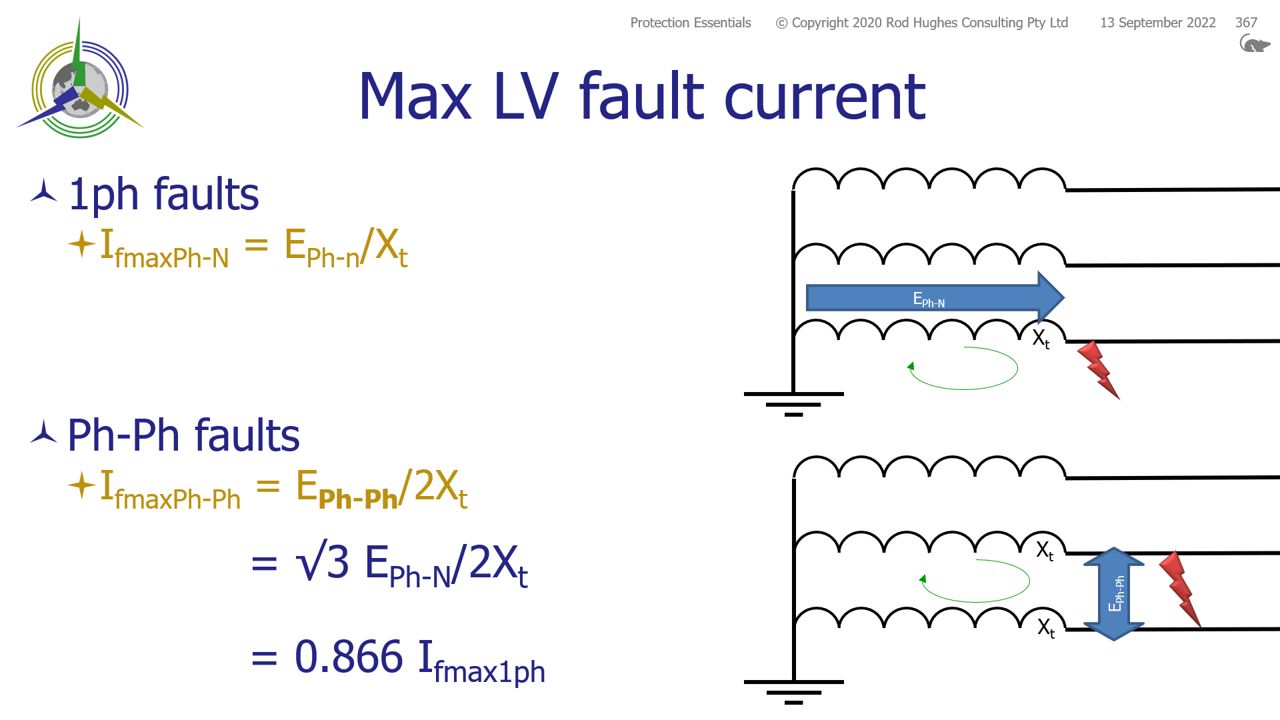

We can see that a phase-to-phase fault has a lower maximum fault current:

I_fmaxPh-Ph = 11000 / (2 x 6.35)  =  866 A.

Hence for a phase-to-phase fault, the LV side inverse time relay will operate slower than for a single phase to earth fault at the same location.

We can now consider these two fault scenarios reflected onto the HV side

1-phase faults on LV

As well as satisfying volt/turn balance on the windings, all transformers also have to satisfy ampere.turn balance.

For a single phase ot earth fault we can therefore calculate the current in the one winding of the HV delta

A_HVwinding x T_HV   =   A_LVwinding x T_LV

A_HVwinding = A_LVwinding x T_LV / T_HV

                   = 1000 x 500 / 866

                   = 577 A

Now because there is no current in two of the delta windings, the current in the other winding can only come from and go to the two lines connected to the end of that winding. 
Hence this is seen as a phase-to-phase fault by the protection on the lines.
The current distribution on the HV lines is 1-1-0, i.e. two phase have equal and opposite 577 A.

The grading margin is now between the operating time of the LV relay at 1000 A compared to the operating time of the HV relay at 577 A, which is of course much slower operating time with the lower current.

Ph-Ph fault on the LV

We must also consider the effect of a phase-to-phase fault on the LV and the respective currents seen on the HV.

As shown above, the maximum LV fault current for a phase-to-phase fault is √3/2 x maximum 1-ph fault, i.e. 866 A.

There are two LV windings involved in the LV fault, therefore two windings of the delta must be carrying current according to ampere.turns balance.

A_HVwinding = A_LVwinding x T_LV / T_HV

                   = 866 x 500 / 866

                   = 500 A

Now consider where the delta winding currents come from and goes to.  

We know that the two LV winding currents are equal and opposite.
Hence the HV winding currents must be equal and opposite.

Hence on two phases, the two line currents equals the winding current.

Whilst on the third phase, the total current is twice the winding current.

Hence for a 866 A phase-to-phase fault on the LV, the HV line current is 500 A on two phases, and 1000 A on the third, so the grading is between 866 A LV and 1000 A HV ..

i.e. the LV inverse relay is operating slower than for a single phase LV fault (866 A c.f. 1000 A) whilst the HV is much faster than for a single phase LV fault (1000 A c.f. 577 A)

Extra Notes: